B.Sc. Psychologie Statisik I
Einleitung
Statistik I umfasst Grundlagen der Wahrscheinlichkeitstheorie, Datenmanagement, sowie diverse deskriptive Statistiken und wie sie in R angewendet werden können.
Diese Zusammenfassung basiert auf der Vorlesung Statistik I im Wintersemester 2023/24 an der PHB bei Professor Robert Miller, sowie dem Lehrbuch “Statistik und Forschungsmethoden” von Eid, Gollwitzer und Schmitt (5.Auflage).
Wahrscheinlichkeitstheorie
Axiome der Wahrscheinlichkeit
Nicht-Negativät
Eine Wahrscheinlichkeit \(Pr\) eines Ereignisses \(E\) ist nie negativ.
\[Pr(E) \ge 0\]
Normalisierung
Die Summe der Wahrscheinlichkeiten \(Pr\) aller Ereignisse \(E_{i}\) in der Menge \(S\) der möglichen Ereignisse ist 1.
\[E_{i} \in S, Pr(S) = 1\]
\[\sum_{i=1}^{n} Pr(E_{i}) = 1\]
Additivität
Die Wahrscheinlichkeit \(Pr\) von wechselseitig ausschließlichen (\(\cup\)) Ereignissen \(E_{i}\) entspricht ihrer Summe.
\[Pr(E_{1} \cup E_{2} \cup \dots) = Pr(E_{1}) + Pr(E_{2}) + \dots\]
Verkettung von Wahrscheinlichkeiten
Wahrscheinlichkeiten von Eriegnissen, die gemeinsam auftreten (\(\cap\)) werden multiupliziert, um die Gesamtwahrscheinlichkeit zu ermitteln.
\[Pr(E_{1} \cap E_{2} \cap \dots) = Pr(E_{1}) \cdot Pr(E_{2}) \cdot \dots\]
Datenmanagement
Querformat/Langformat
Daten in Querformat: mehre Messungen des gleichen Merkmals in jeweils eigener Spalte
tibble(
code = c(1,2,3,4,5),
measurement.1 = rnorm(n = 5, mean = 100, sd = 10),
measurement.2 = rnorm(n = 5, mean = 100, sd = 10),
measurement.3 = rnorm(n = 5, mean = 100, sd = 10)
) -> wide| code | measurement.1 | measurement.2 | measurement.3 |
|---|---|---|---|
| 1 | 112.62954 | 84.60050 | 107.63593 |
| 2 | 96.73767 | 90.71433 | 92.00991 |
| 3 | 113.29799 | 97.05280 | 88.52343 |
| 4 | 112.72429 | 99.94233 | 97.10538 |
| 5 | 104.14641 | 124.04653 | 97.00785 |
Umwandlung in Langformat: Jede Messung in einer eigenen Zeile
wide %>%
pivot_longer(
cols = starts_with("measurement."),
names_prefix = "measurement.",
names_to = "measurement"
) -> long| code | measurement | value |
|---|---|---|
| 1 | 1 | 112.62954 |
| 1 | 2 | 84.60050 |
| 1 | 3 | 107.63593 |
| 2 | 1 | 96.73767 |
| 2 | 2 | 90.71433 |
| 2 | 3 | 92.00991 |
| 3 | 1 | 113.29799 |
| 3 | 2 | 97.05280 |
| 3 | 3 | 88.52343 |
| 4 | 1 | 112.72429 |
| 4 | 2 | 99.94233 |
| 4 | 3 | 97.10538 |
| 5 | 1 | 104.14641 |
| 5 | 2 | 124.04653 |
| 5 | 3 | 97.00785 |
Winsorisierung
- Werte außerhalb eines gewählten Intervalls werden abgeschnitten und durch auf die jeweilige nächste Intervallgrenze gesetzt
- verändert Mittelwert, Varianz und damit auch Standard-Abweichung
- verändert nicht den Median (sofern dieser nicht mit abgeschnitten wurde)
c(0, 1,2,3,4,5,6,7,8,9) %>% ifelse(. > 6, yes = 6, no = .)## [1] 0 1 2 3 4 5 6 6 6 6Häufigkeitstabelle
- absolute Häufigkeit
- kumulierte absolute Häufigkeit
- relative Häufigkeit
- kumulierte relative Häufigkeit
- meistens nach einem Merkmal sortiert
Beispiel: Häufigkeiten von Stürmen nach Jahr
data.short %>%
group_by(year) %>%
summarize(absolute = n()) %>%
ungroup() %>%
arrange(year) %>%
mutate(
absolute.cumulative = cumsum(absolute),
relative = absolute / sum(absolute),
relative.cumulative = cumsum(relative)
) %>% (knitr::kable)| year | absolute | absolute.cumulative | relative | relative.cumulative |
|---|---|---|---|---|
| 2010 | 402 | 402 | 0.1323239 | 0.1323239 |
| 2011 | 323 | 725 | 0.1063199 | 0.2386438 |
| 2012 | 454 | 1179 | 0.1494404 | 0.3880843 |
| 2013 | 202 | 1381 | 0.0664911 | 0.4545754 |
| 2014 | 139 | 1520 | 0.0457538 | 0.5003292 |
| 2015 | 220 | 1740 | 0.0724161 | 0.5727452 |
| 2016 | 396 | 2136 | 0.1303489 | 0.7030941 |
| 2017 | 306 | 2442 | 0.1007242 | 0.8038183 |
| 2018 | 266 | 2708 | 0.0875576 | 0.8913759 |
| 2019 | 330 | 3038 | 0.1086241 | 1.0000000 |
Split-Apply-Combine
- Split: Daten nach einem Merkmal gruppieren
- Apply: Aggregation ausführen (zb Summen, Mittelwerte, Minima/Maxima)
- Combine: Gruppierung aufheben
data.short %>%
group_by(name) %>%
summarize(wind.top = max(wind)) %>%
ungroup() %>%
arrange(-wind.top) %>%
top_n(10) %>%
(knitr::kable)| name | wind.top |
|---|---|
| Dorian | 160 |
| Maria | 150 |
| Matthew | 145 |
| Lorenzo | 140 |
| Michael | 140 |
| Igor | 135 |
| Joaquin | 135 |
| Gonzalo | 125 |
| Julia | 120 |
| Katia | 120 |
| Nicole | 120 |
| Ophelia | 120 |
Stratifizierung
Daten mit kontinuierlichen Merkmalen oder sehr vielen diskreten Ausprägungen werden in Strata (Gruppen) zusammengefasst, zB. um dann aggregierte Werte (Mittelwerte, Min/Max, etc.) in jeder Gruppe zu berechnen.
Beispiel: höchste Windgeschwindigkeit nach Jahrzehnt
data.long %>%
mutate(
decade = cut(
year,
breaks = seq(1970, 2030, 10),
labels = paste0(seq(1970, 2020, 10), "s"),
include.lowest = TRUE,
right = FALSE
)
) %>%
group_by(decade) %>% summarize(top.wind = max(wind)) %>%
(knitr::kable)| decade | top.wind |
|---|---|
| 1970s | 150 |
| 1980s | 160 |
| 1990s | 155 |
| 2000s | 160 |
| 2010s | 160 |
| 2020s | 135 |
Zentrale Tendenz
Mittelwert/Durchschnitt
- Summe aller einzelnen Werte, geteilt durch die Anzahl der Werte.
- mindestens intervallskaliert
- anfällig für Extremwerte
- übliches Symbol für Mittelwert einer Population: \(\mu\)
- übliches Symbol für Mittelwert einer Stichprobe: \(\overline{x}\)
\[\overline{x} = \frac{1}{n}\cdot\sum_{i=1}^{n} n_{i}\]
mean(data.long$pressure)## [1] 991.9805Modus
- Wert mit der größten absoluten Häufigkeit
- alle Skalenniveaus
data.long %>% group_by(month) %>% summarize(n = n()) %>% arrange(-n) %>% top_n(1)## Selecting by n## # A tibble: 1 × 2
## month n
## <dbl> <int>
## 1 9 4894Median
- Wert, der wenn alle Werte sortiert sind, in der Mitte steht. Bei gerader Anzahl stehen zwei Werte in der Mitte. Dann wird aus diesen der Mittelwert gebildet.
- midnestens ordinalskaliert
Ungerade Anzahl:
\[1, 2, 2, 4, \color{red}{5}, 5, 7, 8, 9\]
Gerade Anzahl:
\[1, 2, 2, 3, \color{red}{3}, \color{red}{5}, 5, 7, 8, 9\] \[\frac{3+5}{2} = \color{red}{4}\]
median(data.long$pressure)## [1] 999Dispersion
Variationsbreite
- Intervall aus Minimum und Maximum
\[\color{red}{1}, 2, 2, 4, 5, 5, 7, 8, \color{red}{9}\] \[VB = [1,9]\]
range(c(1,2,2,4,5,5,7,8,9))## [1] 1 9Quantile
Quantil: Wertebereich, in dem eine bestimmte Menge der Merkmalsträger liegt, \(Q_{p} \to p \%\)
Terzile: \(Q_{33.3}\), \(Q_{66.6}\), \(Q_{100}\)
Quartile: \(Q_{25}\), \(Q_{50}\), \(Q_{75}\), \(Q_{100}\)
Quintile: \(Q_{20}\), \(Q_{40}\), \(Q_{60}\), \(Q_{80}\), \(Q_{100}\)
Median entspricht \(Q_{50}\), Minimum und Maximum entsprechen \(Q_{0}\) bzw. \(Q_{100}\)
Berechnung
Position des Quantils: \(Q_{p} \to i = n \cdot p\)
Z.B. bei \(n = 200\) für \(Q_{75}\): \(i = 200 * 0.75 = 150\)
Wenn \(i\) ganze Zahl ist, dann ist \(Q_{p} = \frac{x_{i} + x_{i+1}}{2}\) (Mittelwert aus Position \(x_{i}\) und \(x_{i + 1}\))
Wenn \(i\) keine ganze Zahl ist, dann wird \(i\) aufgerundet (\(\lceil i\rceil\)) und \(Q_{p} = x_{\lceil i\rceil}\), der Wert an der jeweils nächst-höheren Stelle.
quantile(data.long$pressure, probs = seq(1/5, 5/5, 1/5)) #quintile## 20% 40% 60% 80% 100%
## 979 994 1002 1007 1022Interquartilsabstand (IQR)
Differenz zwischen erstem und drittem Quartil:
\[IQR = Q_{75} - Q_{25}\]
IQR(data.long$pressure)## [1] 21Varianz
- mittlere quadrierte Abweichung vom Mittelwert
- durch Quadierung werden die Abweichungen alle positiv, d.h. Richtung der Abweichung spielt für Varianz keine Rolle
- bezieht sich auf Gesamtpopulation (siehe Stichprobenvarianz)
- mindestens intervallskaliert
\[\sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^{n} (x_{i} - \overline{x})^2\]
Stichprobenvarianz
- bezieht sich auf Stichproben aus einer Population
- enthält eine Korrektur (\(n - 1\)) gegenüber der allgemeinen Varianz
\[s^2 = \frac{1}{n - 1} \cdot \sum_{i=1}^{n} (x_{i} - \overline{x})^2\] Je größer \(n\), umso mehr nähert sich die Stichprobenvarianz der allgemeinen Varianz an:
\[\lim_{n \to \infty} \frac{1}{n-1} =
\frac{1}{n}\] R berechnet mit var standardmäßig die
Stichproben-Varianz:
var(data.long$pressure)## [1] 382.1348Standardabweichung
- positive Quadratwurzel aus der Varianz
- mindestens intervallskaliert
- bezieht sich auf gesamte Population
\[\sigma = \sqrt{\sigma^2}\]
Bei normalverteilten Merkmalen:
- 68.2% zwischen \(\overline{x}\pm 1\sigma\)
- 95.5% zwischen \(\overline{x}\pm 2\sigma\)
- 99.5% zwischen \(\overline{x}\pm 3\sigma\)
Stichproben-Standardabweichung
- positive Quadratwurzel aus der Stichproben-Varianz
- gleiche Korrektur wie bei Stichproben-Varianz
- bezieht sich auf Stichproben
\[s = \sqrt{s^2}\]
R berechnet mit sd standardmäßig die
Stichproben-Standardabweichung:
sd(data.long$pressure)## [1] 19.54827Variationskoeffizient
- Stichproben-Standardabweichung relativ zum Mittelwert
- verhältnisskaliert
\[CV = \frac{s}{\overline{x}}\]
sd(data.long$pressure) / mean(data.long$pressure)## [1] 0.0197063Histogramm
- gibt schnellen visuellen Eindruck der Verteilung empirischer Daten
data.long %>%
ggplot(aes(x = wind)) +
geom_histogram(bins = 30, color = "white", fill = colors[2]) +
theme_custom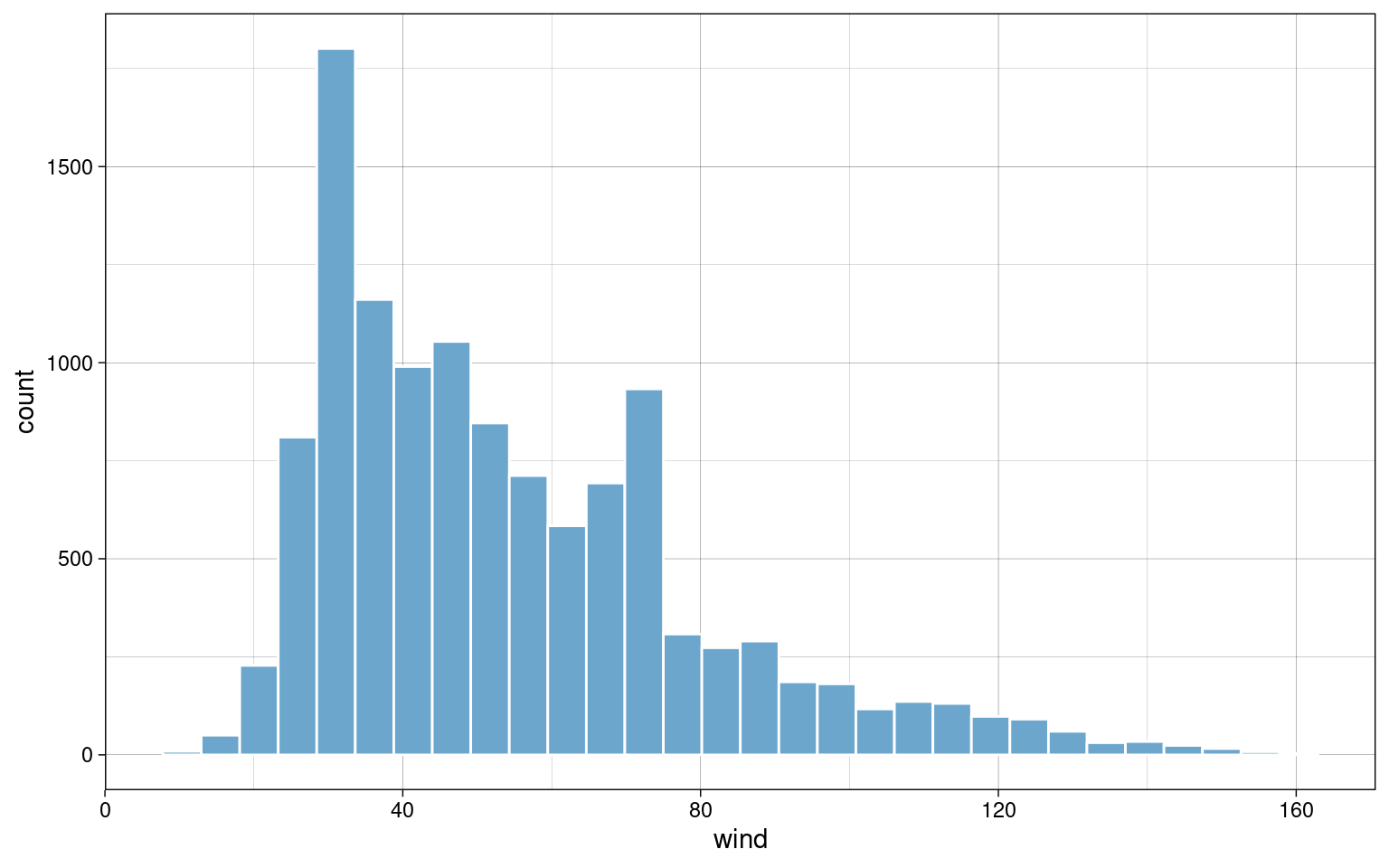
Kerndichteschätzer
- Schätzung der Wahrscheinlihckeitsdichte einer empirischen Verteilung
data.long %>%
ggplot(aes(x = wind)) +
geom_density() +
theme_custom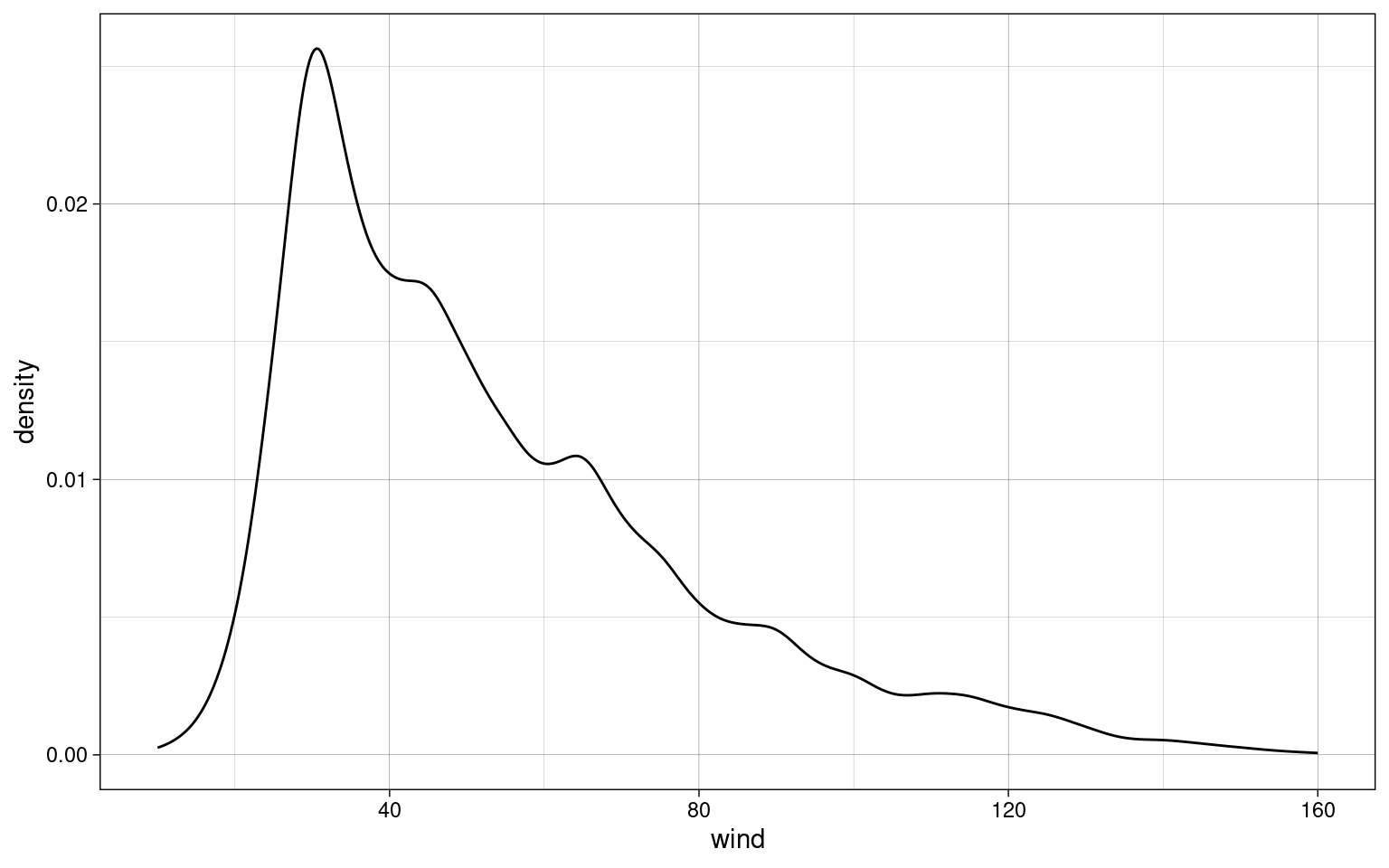
Standardisierung
Durch Standardisierung werden Werte miteinander vergleichbar, auch wenn sie z.B. in unterschiedlichen Größenordnungen oder Einheiten vorliegen.
Z-Werte / Z-Standardisierung
- spielen in vielen weiteren Berechnungen eine sehr große Rolle
Alle einzelnen Werte werden auf 0 zentriert und so skaliert, dass sie eine Standardabweichung von 1 haben:
\[z_{i} = \frac{x_{i} - \overline{x}}{s}\]
data.short %>% select(wind) %>%
mutate(wind.z = (wind - mean(wind))/sd(wind))## # A tibble: 3,038 × 2
## wind wind.z
## <int> <dbl>
## 1 30 -0.988
## 2 30 -0.988
## 3 40 -0.576
## 4 40 -0.576
## 5 55 0.0403
## 6 55 0.0403
## 7 55 0.0403
## 8 45 -0.371
## 9 35 -0.782
## 10 40 -0.576
## # ℹ 3,028 more rowsProzentränge
- geben an, wieviel Prozent einer Häufigkeitsverteilung den gleichen oder einen niedrigeren Wert in einem Merkmal haben
- mindestens intervallskaliert
- basiert auf Z-Werten
data.short %>% select(wind) %>%
mutate(
wind.z = (wind - mean(wind))/sd(wind),
wind.pr = pnorm(wind.z)
)## # A tibble: 3,038 × 3
## wind wind.z wind.pr
## <int> <dbl> <dbl>
## 1 30 -0.988 0.162
## 2 30 -0.988 0.162
## 3 40 -0.576 0.282
## 4 40 -0.576 0.282
## 5 55 0.0403 0.516
## 6 55 0.0403 0.516
## 7 55 0.0403 0.516
## 8 45 -0.371 0.355
## 9 35 -0.782 0.217
## 10 40 -0.576 0.282
## # ℹ 3,028 more rowsRang-basierte Normalisierung
- reduziert Skalenniveau zu ordinal
- erzeugt normalverteilte Werte
- sehr effektiv gegen Extremwerte, ohne sie komplett zu entfernen
Schritt 1: Werte sortieren
## # A tibble: 10 × 1
## x
## <dbl>
## 1 1
## 2 1
## 3 2
## 4 3
## 5 3
## 6 3
## 7 4
## 8 4
## 9 4
## 10 5Schritt 2: Ränge zuordnen
Bei gleichen Werten wird ein Rang mehrfach vergeben
## # A tibble: 10 × 2
## x n
## <dbl> <int>
## 1 1 1
## 2 1 2
## 3 2 3
## 4 3 4
## 5 3 5
## 6 3 6
## 7 4 7
## 8 4 8
## 9 4 9
## 10 5 10Schritt 3: bei geteilten Rängen Mittelwert bilden
## # A tibble: 10 × 3
## x n r
## <dbl> <int> <dbl>
## 1 1 1 1.5
## 2 1 2 1.5
## 3 2 3 3
## 4 3 4 5
## 5 3 5 5
## 6 3 6 5
## 7 4 7 8
## 8 4 8 8
## 9 4 9 8
## 10 5 10 10Schritt 4: Prozentränge und Z-Werte berechnen
\[y = \frac{r-0.5}{n}\]
## # A tibble: 10 × 5
## x n r p z
## <dbl> <int> <dbl> <dbl> <dbl>
## 1 1 1 1.5 0.1 -1.28
## 2 1 2 1.5 0.1 -1.28
## 3 2 3 3 0.25 -0.674
## 4 3 4 5 0.45 -0.126
## 5 3 5 5 0.45 -0.126
## 6 3 6 5 0.45 -0.126
## 7 4 7 8 0.75 0.674
## 8 4 8 8 0.75 0.674
## 9 4 9 8 0.75 0.674
## 10 5 10 10 0.95 1.64Nach der Rang-basierten Normalisierung sind \(p\) und \(z\) normalverteilt.
Bedingte Wahrtscheinlichkeit
Bedingte Wahrscheinlichkeit \(Pr(B|A)\) ist die Wahrscheinlichkeit, dass A und B gemeinsam auftreten (\(A \cap B\)) unter der Bedingung, dass A bereits eingetreten ist, z.B. die Wahrscheinlichkeit, dass eine Person tatsächlich schwanger ist (B), wenn ein Schwangerschaftstest positiv ausgefallen ist (A).
\[Pr(A|B) = \frac{Pr(A \cap B)}{Pr(A)}\]
Bayes-Theorem
Das Bayes-Theorem stellt den Zusammenhang zwischen den bedingten Wahrscheinlichkeiten \(Pr(B|A)\) und \(Pr(A|B)\) her:
\[Pr(A|B) = \frac{Pr(B|A) \cdot Pr(A)}{Pr(B)}\]
Kontingenztabellen
Kontingenztabellen sind ein Mittel, um Bedingte Wahrscheinlichkeiten zu untersuchen. Die Tabelle enthält alle möglichen Kombinationen zweier diskreter Variablen und deren Häufigkeiten.
Beispiel Schwangerschaftstest:
\(A_+\): Test positiv
\(A_-\): Test negativ
\(B_+\): Schwangerschaft liegt vor
\(B_-\): Schwangerschaft liegt nicht vor
\(A_+ \cap B_-\): falsch-positiver Test
\(A_- \cap B_-\): falsch-negativer Test
\(A_- \cap B_-\): richtig-negativer Test
\(A_+ \cap B_+\): richtig-positiver Test
(fiktive Daten)
## A+ A-
## B+ 208 19
## B- 11 762Randsummen stellen jeweils die Summe der Häufigkeiten in jeder Zeile und Spalte, also die Einzelwahrscheinlichkeiten \(Pr(A_+), Pr(A_-), Pr(B_+), Pr(B_-)\).
Die Randsummen können in R automatisch ermittelt werden:
addmargins(samples)## A+ A- Sum
## B+ 208 19 227
## B- 11 762 773
## Sum 219 781 1000Ausgedrückt als relative Häufigkeiten:
addmargins(samples) / sum(samples)## A+ A- Sum
## B+ 0.208 0.019 0.227
## B- 0.011 0.762 0.773
## Sum 0.219 0.781 1.000Sensitivität
Sensitivität ist die Wahrscheinlichkeit, dass ein Test eine tatsächlich vorliegende Merkmalsausprägung auch erfasst.
Im Beispiel: dass bei vorliegender Schwangerschaft (\(B_+\)), der Test positiv ausfällt (\(A_+\))
\[Pr(A_+|B_+) = \frac{Pr(A_+ \cap B_+)}{Pr(B_+)}\]
\[Pr(A_+|B_+) = \frac{0.208}{0.227} \approx 0.916 \]
Spezifität
(engl.: specificity)
Spezifität ist die Wahrscheinlichkeit, dass eine nicht vorhandene Ausprägung zu einem negativen Testergebnis führt.
Im Beispiel: dass bei nicht vorhandener Schwangerschaft der Test negativ ausfällt
\[Pr(A_-|B_-) = \frac{Pr(A_- \cap B_-)}{Pr(B_-)}\]
\[Pr(A_-|B_-) = \frac{0.762}{0.773} \approx 0.987 \]
Sensitivität und Spezifität geben NICHT an, ob eine positiv ode negativ ausgefallener Test zuverlässig ist. Dafür sind PPV und NPV relevant.
Positiver Vorhersagewert
(engl.: positive preditive value, PPV)
Der PPV gibt an wie wahrscheinlich eine Merkmalsausprägung bei einem positiven Test vorliegt.
Im Beispiel: wie wahrscheinlich jemand bei einem positiver Schwangerschaftstest tatsächlich schwanger ist.
\[Pr(B_+|A_+) = \frac{Pr(B_+ \cap A_+)}{Pr(A_+)}\]
\[Pr(B_+|A_+) = \frac{0.762}{0.781} \approx 0.976 \]
Negativer Vorhersagewert
(engl.: negative predictive value, NPV)
Der NPV gibt an wie wahrscheinlich bei einem negativen Test die getestete Merkmalsausprägung auch tatsächlich nicht vorliegt.
Im Beispiel: wie wahrscheinlich eine negativer Schwangerschaftstest bedeutet, dass die getestete Person wirklich nicht schwanger ist.
\[Pr(B_-|A_-) = \frac{Pr(B_- \cap A_-)}{Pr(A_-)}\]
\[Pr(A_-|B_-) = \frac{0.762}{0.773} \approx 0.987 \]
Weitere Test-Charakteristiken
- Falsch-Positiv-Rate: \(1 - Spezifität\), weil \(Pr(B_-|A_+) + Pr(B_+|A_+) = 1\)
- Falsch-Negativ-Rate: \(1 - Sensitivität\), weil \(Pr(B_+|A_-) + Pr(B_-|A_-) = 1\)
Korrelation
Korrelation beschreibt den Zusammenhang zwischen zwei Merkmalen, also wie stark eine Merkmal sich ändert, wenn ein damit korreliertes geändert wird.
Korrelationskoeffizienten sind normierte Maße für die beobachteten Zusammenhänge zwischen Variablen. Sie treffen jedoch keine Aussage über kausale Zusammenhänge.
Beispiel: Alter von Kindern und Körpergröße
Die meisten Kinder werden mit zunehmendem Alter größer. Alter und Größe sind positiv korreliert.
Es existieren verschiedene Korrelationsmaße für verschiedene Einsatzfälle.
| Korrelationsmaß | Skalenniveau |
|---|---|
| Matthew-Phi Chancenverhältnis |
Nominal (dichotom ) |
| Chi-Quadrat Cramer-V |
Nominal (polytom) |
| Spearman-Rho Kendall-Tau |
mindestens Ordinal |
| Bravais-Pearson (Produkt-Moment-Korrelation) |
minestens Intervall |
Matthew-Korrelationskoeffizient
- geeignet für nominal-skalierte Merkmale mit je zwei Ausprägungen (dichotom).
- Wertebereich: \([-1, +1]\)
- bei \(\phi = 0\) besteht kein Zusammenhang zwischen den Merkmalen
| \(A_1\) | \(A_2\) | |
|---|---|---|
| \(B_1\) | \(n_{1,1}\) | \(n_{1,2}\) |
| \(B_2\) | \(n_{2,1}\) | \(n_{2,2}\) |
\[\phi = \frac{n_{1,1} \cdot n_{2,2} - n_{1,2} \cdot n_{2,1}}{\sqrt{(n_{1,1} + n_{2,1}) \cdot (n_{1,2} + n_{2,2}) \cdot (n_{1,2} + n_{2,1}) \cdot (n_{2,1} + n_{2,2})}}\]
Chancenverhältnis (Odds Ratio)
- geeignet für nominal-skalierte Merkmale mit je zwei Ausprägungen (dichotom)
- Wertebereich: \([0, +\infty]\)
- bei \(OR = 1\) besteht kein Zusammenhang zwischen den Merkmalen
Eine Chance ist das Verhältnis zweier Häufigkeiten
\[OR = \frac{\frac{n_{1,1}}{n_{1,2}}}{\frac{n_{2,1}}{n_{2,2}}} = \frac{n_{1,1} \cdot {n_{2,2}}}{n_{1,2} \cdot n_{2,1}}\]
Chi-Quadrat-Koeffizient
- geeignet für nominal-skalierte Merkmale mit mehreren Ausprägungen (polytom)
- Wertebereich: \([0, +\infty]\)
- bei \(\chi^2 = 0\) besteht kein Zusammenhang zwischen den Merkmalen
- \(\chi^2\) gibt keine Auskunft über die Richtung des Zusammenhangs
- abhängig von der Stichprobengröße
\[\chi^2 = \sum_{i=1}^k\sum_{j = 1}^l\frac{(n_{ij} - e_{ij})^2}{e_{ij}}\] \(e_{ij}\) ist die erwartete Häufigkeit unter der Annahme, dass kein Zusammenhang besteht:
\[e_{ij} = \frac{n_i \cdot n_j}{n}\]
Cramer’s-V-Koeffizient
- abgeleitet von \(\chi^2\)
- geeignet für nominal-skalierte Merkmale mit mehreren Ausprägungen (polytom)
- Wertebereich: \([0,1]\)
- bei \(V = 0\) besteht kein Zusammenhang zwischen den Merkmalen
- \(V\) gibt keine Auskunft über die Richtung des Zusammenhangs
- unabhängig von der Stichprobengröße
\[V = \sqrt{\frac{\chi^2}{n \cdot (s-1)}}\]
\(s\) ist die kleinere Anzahl an Kategorien (Ausprägungen) der Variablen. Wenn z.B. eine Variable 5 Kategorien aufweist, die andere jedoch nur 3, so ist \(s=3\).
Spearman-Rho-Korrelationskoeffizient
- geeignet für ordinal-skalierte Variablen mit Rangbindung, bzw. rang-transformierte metrische Variablen
- Wertebereich: [-1, +1]
- bei \(\rho = 0\) besteht kein Zusammenhang
\[\rho = \frac{1}{n-1}\sum_{i=1}^{n}{\frac{(r_{i,1} - \overline{x}_1)}{s_1} \cdot \frac{(r_{i,2} - \overline{x}_2)}{s_2}}\] - \(r_{i,1}\), \(r_{i,2}\): rang-transformierte Ausprägungen von Merkmal 1 und 2 - \(\overline{x}_1\), \(\overline{x}_2\): arithmetische Mittel der Rangreihe 1 und 2 - \(s_1\), \(s_2\): Stichproben-Standardabweichungen der Rangreihen 1 und 2 - \(n\): Anzahl der Zeilen (Stichprobengröße)
\(\rho\) ist vereinfacht die mittlere Produktsumme der z-transformierten Rangwerte:
\[\rho = \frac{1}{n-1}\sum_{i=1}^{n}{z_1 \cdot z_2}\]
Kendall’s-Tau-Korrelationskoeffizient
- geeignet für ordinal-skalierte Variablen ohne Rangbindung
- ohne Modifikation nicht geeignet, wenn geteilte Ränge vorliegen
- Wertebereich: [-1, +1]
- bei \(\tau = 0\) besteht kein Zusammenhang
\[\tau = \frac{n_K - n_D}{n_k + n_D}\] - \(n_K\): Anzahl der konkordanten Paarvergleiche - \(n_D\): Anzahl der Diskordanten Paarvergleiche
Konkordanz/Diskordanz:
Eine Tabelle mit beiden ordinalen Merkmalen (A und B) wird nach Merkmal A aufsteigend sortiert:
| A | B |
|---|---|
| 24 | 35 |
| 32 | 42 |
| 36 | 24 |
| 42 | 29 |
| 54 | 61 |
| 58 | 53 |
| 59 | 78 |
| 74 | 69 |
| 74 | 73 |
| 76 | 84 |
Anschließend wird Zeilenweise verglichen, wie viele nachfolgende Werte in Spalte B größer sind als B in der aktuellen Zeile. Z.B in Zeile 1 ist \(B=35\) und 7 der darauf folgenden Werte in Spalte B (42, 61, 53, 78, 69, 73, 84) sind größer, diese sind konkordante Paare. Paare, bei denen der weiter unten stehende Wert kleiner ist, sind diskordant. Beide werden ausgezählt.
| A | B | konkordant | diskordant |
|---|---|---|---|
| 24 | 35 | 7 | 2 |
| 32 | 42 | 6 | 2 |
| 36 | 24 | 7 | 0 |
| 42 | 29 | 6 | 0 |
| 54 | 61 | 4 | 1 |
| 58 | 53 | 4 | 0 |
| 59 | 78 | 1 | 2 |
| 74 | 69 | 2 | 0 |
| 74 | 73 | 1 | 0 |
| 76 | 84 | 0 | 0 |
Dann werden die Anzahlen der konkordanten und diskordanten Paare summiert:
## $n_k
## [1] 38
##
## $n_d
## [1] 7Kovarianz
- geeignet für metrische Variablen
- Wertebereich: \([0, +\infty]\)
- keine Korrelation
- empfindlich für Extremwerte
\[COV = \frac{1}{n-1} \cdot \sum_{i=1}^n{(x_{i,1} - \overline{x}_1)\cdot((x_{i,2} - \overline{x}_2)}\]
Analog zur Stichprobenvarianz. Diese ist die Kovarianz eines Merkmals mit sich selbst.
Bravais-Pearson-Korrelationskoeffzient
- geeignet für metrische Variablen
- abgeleitet aus der Kovarianz
- Wertebereich: \([-1, +1]\)
\[r = \frac{COV}{s_1 \cdot s_2} = \frac{1}{n-1} \cdot \sum_{i=1}^n{\frac{(x_{i,1} - \overline{x}_1)}{s_1} \cdot \frac{(x_{i,2} - \overline{x}_2)}{s_2}}\]
Analog zu Spearman-\(\rho\) ist auch \(r\) die mittlere Produktsumme der Z-Werte der beiden Merkmale:
\[r = \frac{1}{n-1}\sum_{i=1}^{n}{z_1 \cdot z_2}\]
Modellbildung
Modelle beschreiben eine idealisierte Verteilung von Merkmalen in einer Population und sind durch ihre Parameter definiert.
Beispiele:
| Modell | Parameter |
|---|---|
| Normalverteilung | Standardabweichung \(\sigma\) Mittelwert \(\mu\) |
| Student-t-Verteilung | Freiheitsgrade \(df\) |
| Binomialverteilung | Einzelwahrscheinlichkeit \(p\) Ziehungszahl \(n\) |
Parameterschatzung durch Likelihood-Maximierung
Die Likelihood ist die verkettete Wahrscheinlichkeit des Auftretens aller beobachteten Ausprägungen unter der Annahme bestimmter Modellparameter:
\[Lik = \prod_{i = 1}^n x_n = Pr(x_1) \cdot Pr(x_2) \cdot \ldots \cdot Pr(x_n)\]
Da Wahrscheinlichkeiten immer \(\le 1\) sind, wird die Likelihood oft eine sehr kleine Zahl. Um sie besser handhaben zu können und Präzisionsprobleme bei der Auswertung mit Computern zu vermeiden, wird sie oft logarithmiert (mit dem natürlichen Logarithmus \(log_e(x)\)) als Log-Likelihood (\(LogLik\)). Nach den Logarithmengesetzen (Produktregel) ist \(LogLik\) die Summe der logarithmierten Wahrscheinlichkeiten:
\[LogLik = log(Lik) = \sum_{i=1}^n log(Pr(x_n))\]
Hinweis: die Log-Likelihood ist immer negativ, weil Wahrscheinlichkeiten immer \(\le 1\) sind. Das kann zu Irrtümern bei der Maximierung führen, da kleinere negative Zahlen eine größeren Betrag haben (z.B. \(-8253 \lt -2417\)).
Die maximale Likelihood wird meist numerisch bestimmt. Ein einfaches Verfahren ist, die Likelihood für Werte der Modellparameter in einem bestimmten Bereich zu testen und dann das Maximum durch Sortierung zu finden.
Beispiel:
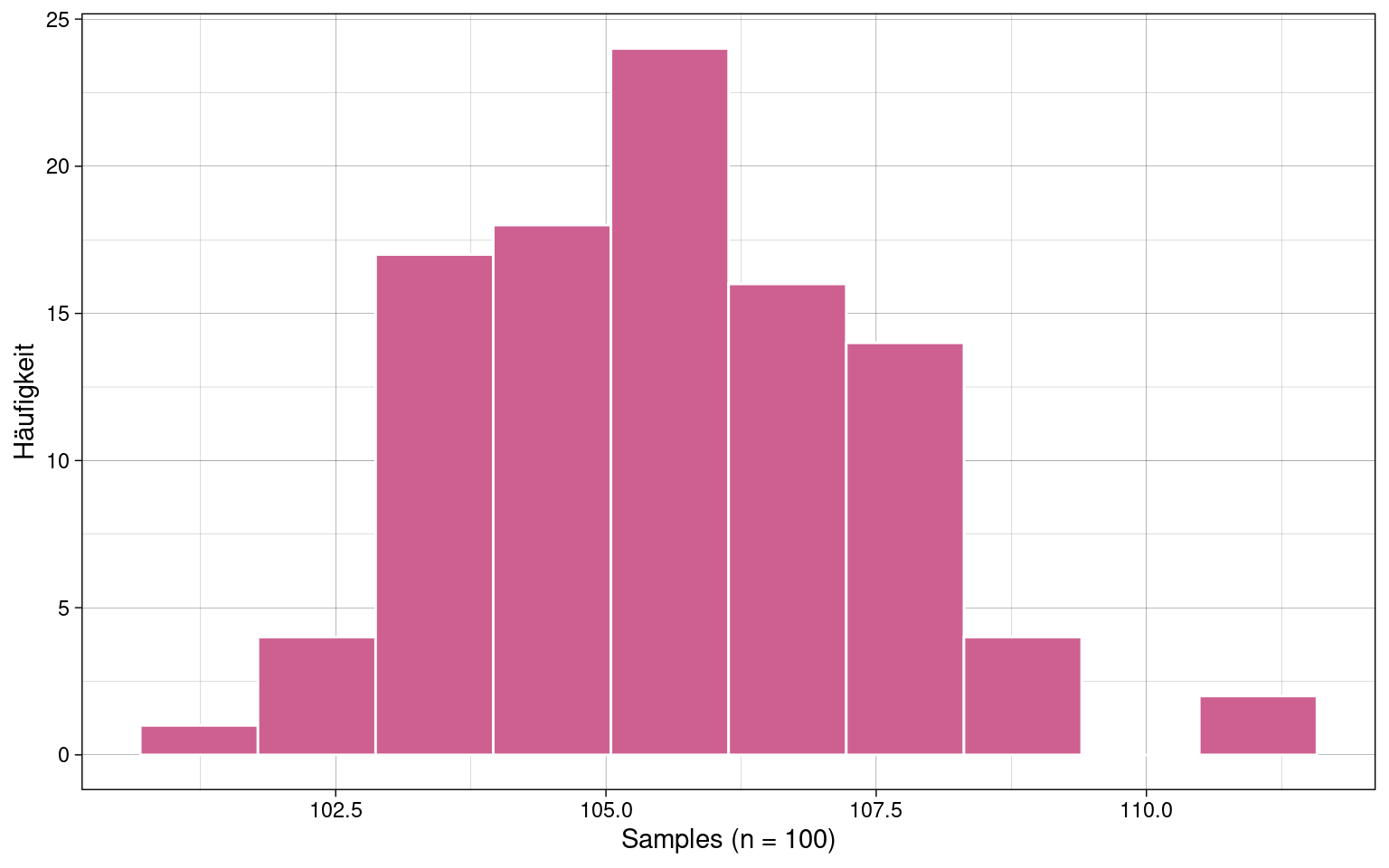
Anhand des Histogramms, wird der Mittelwert bei ca. 106 vermutet, die Standardabweichung bei 2.
Modellanpassung einer Normalverteilung mittels Optimierung in R:
# Berechnung der LogLikelihood der Samples in einer Funktion
loglik_samples <- function(params) {
m <- params[1]
s <- params[2]
sum(log(dnorm(samples, mean = m, sd = s)))
}
optim(
c(106,2), # initiale vermutete Werte, mit denen die Optimierung beginnt
loglik_samples, # Funktion, die optimiert werden soll
control = list(fnscale = -1) # Einstellung für Maximierung statt Minimierung
)## $par
## [1] 105.647904 1.844083
##
## $value
## [1] -203.1024
##
## $counts
## function gradient
## 65 NA
##
## $convergence
## [1] 0
##
## $message
## NULLPower-Transformationen
- erzeugt Werte die näher an einer Normalverteilung liegen
- nur für positive Ausprägungen geeignet
Power-Transformationen dienen dazu, Daten in einfachere Verteilungen zu überführen (z.B. Normalverteilung).
Ein-Parameter Power-Transformation nach Box & Cox (1964)
\[ y_i(\lambda) = \begin{cases} \frac{y_i^{\lambda}-1}{\lambda} ,& \lambda \ne 0 \\ ln(y_i) ,& \lambda = 0 \end{cases} \]
Der am besten passende Parameter \(\lambda\) kann mittels Likelihood-Maximierung geschätzt werden.
Zwei-Parameter Power-Transformation nach Box & Cox (1964)
- erzeugt Werte die näher an einer Normalverteilung liegen
- nur für positive Ausprägungen geeignet
\[ y_i(\lambda_1, \lambda_2) = \begin{cases} \frac{(y_i + \lambda_2)^{\lambda_1}-1}{\lambda_1} ,& \lambda_1 \ne 0 \\ ln(y_i + \lambda_2) ,& \lambda_1 = 0 \end{cases} \]
Power-Transformation nach Yeo & Johnson (2000)
- erzeugt Werte die näher an der Normalverteilung liegen
- auch geeignet für negative Ausprägungen
\[ y_i(\lambda) = \begin{cases} ((y_i + 1) ^\lambda -1) / \lambda ,& \lambda \ne 0, y \ge 0 \\ ln(y_i +1) ,& \lambda = 0, y \ge 0\\ -((-y_i + 1)^{2-\lambda}-1) / (2-\lambda) ,& \lambda \ne 2, y \lt 0 \\ -ln(-y_i +1) ,& \lambda = 2, y \lt 0 \end{cases} \]
